Numerical Analysis of Prebunking Algorithms

Table of Links

Abstract and Introduction

Related Works

Preliminaries

Optimal Prebunking Problem

Deterministic Baseline Policies

Temporally Equidistant Prebunking

Numerical Results

Conclusion and References

VII. NUMERICAL RESULTS

A. Algorithm Comparison

We compare Algorithms 1, 2, and 3 by evaluating their performance on simulated misinformation propagations in large scale-free networks. We simulate the misinformation propagation as an SI process on a Chung-Lu model [23].

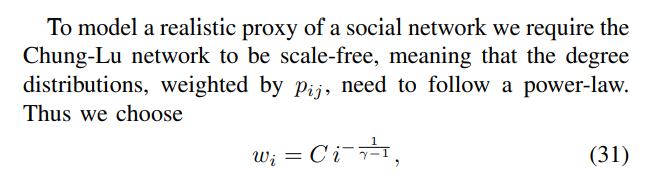
where C and γ are tunable parameters. By Lemma 3.0.1 from Fasino et al. [24], this choice for wi guarantees the resulting Chung-Lu model is scale-free.

We selected the parameters C and γ by tuning them so that at each step, the resulting SI propagation most closely resembles the daily message propagation in a real social networking platform. To do so, we chose the Twitter WICO dataset [25], which is a collection of timestamped propagations containing tweets/re-tweets, in two misinformation and one non-misinformation categories. We then tuned the the parameters C and γ so that the number of infected users in the simulated SI cascade on the resulting Chung-Lu model matches the misinformation propagation in the WICO dataset. Fig. 1 shows a small example of this Chung-Lu network consisting of 100 users.

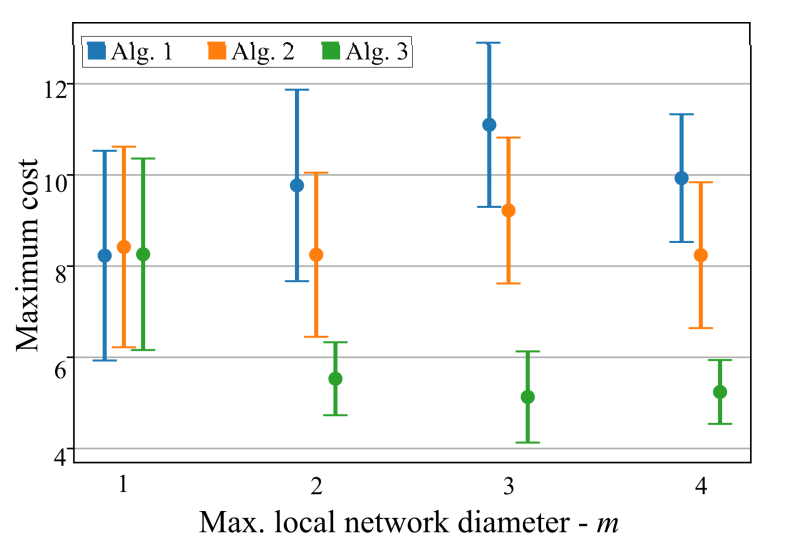
We test each algorithm by first choosing random user to guard against misinformation, which we call c as before. We then construct a local neighborhood of radius m around c by finding the subgraph containing all users that are at most m graph distance away from c. Fig. 2 shows the distributions of the accumulated maximal cost C(A) across four different choices of m. For each m we repeat the experiment 10 times and plot the mean and the deviations of C(A) across these runs.

Fig. 2 shows that Algorithm 3 clearly achieves prebunking with less cost than the baselines, with its average cost being approximately half of the other two algorithms for m ≥ 2. Note that all three algorithms achieve the same cost for m = 1 as the feasibility restrictions force all three algorithms to induce the same policy in this case. That is, their behavior are identical for m = 1. Also note that since the diameter of the original network is 4, we restrict m to be less than 4.

B. Effects of Prebunking on the Misinformation Propagation

So far we have discussed policies to guard a single user c against misinformation by issuing them prebunks before their corresponding misinformation content. In a social networking platform, however, the goal is often to guard as many users as possible against misinformation. In this paper we mainly focus on optimizing the prebunking delivery to a single user since protecting singular users c extends naturally to protect the entire network, as it is possible to significantly reduce the propagation of misinformation by applying these prebunking algorithms to a selected group of users, inoculating them against misinformation and preventing them from spreading misinformation to users they influence.

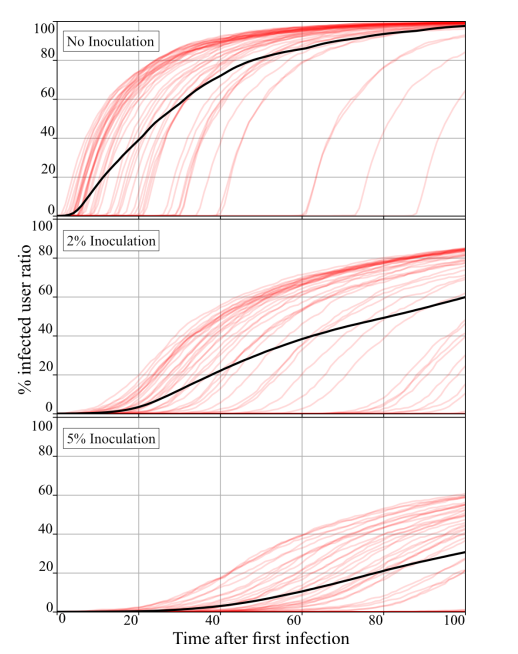
We test the effect of Algorithm 3 on the misinformation propagation by simulating a misinformation cascade on a Chung-Lu network with 2000 users, using the same parameters as in section VII-A. However, instead of providing prebunks to a single user, we provide prebunks to a small subset of users with maximal expected degrees. We show the resulting misinformation propagation curves in Fig. 3. It is evident that applying Algorithm 3 to deliver prebunks to a small number of nodes significantly delays the propagation of misinformation, at least for the scale-free networks with which we are experimenting. This is not surprising in and of itself, as it is consistent with the existing literature which demonstrates that the shortest path lengths between nodes in a scale-free network is often sensitive to the removal of the highly connected nodes [26], [27]. In addition, prebunking reduces the variance between different misinformation cascades, making their propagation more predictable.